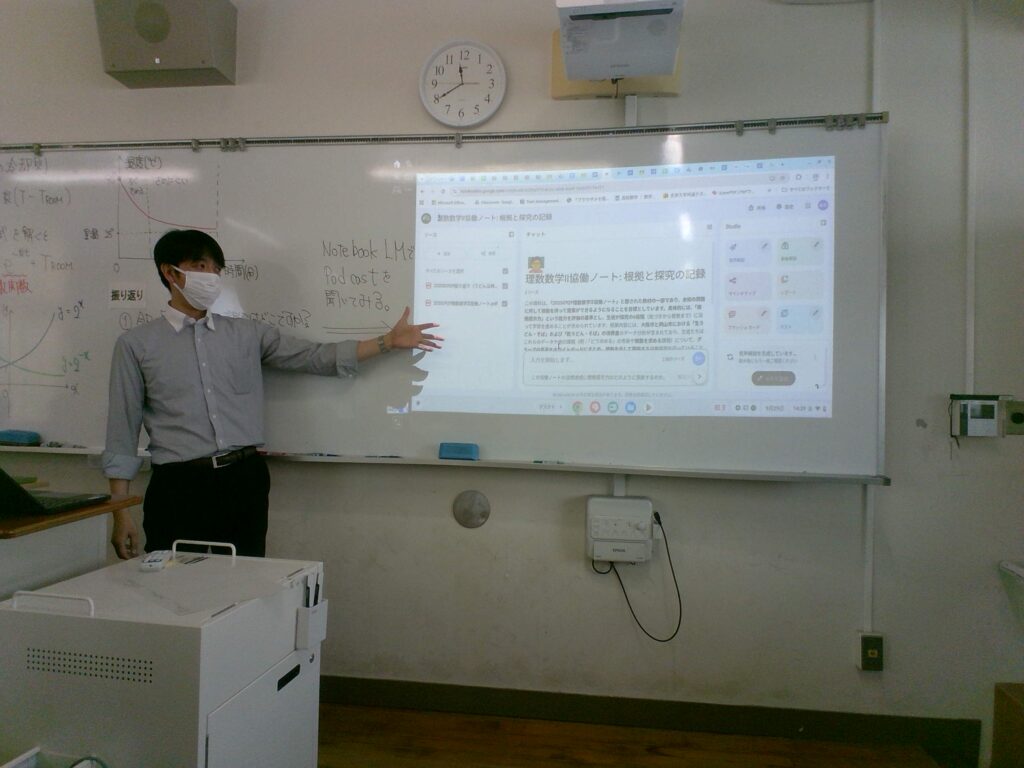
うどんが冷めるスピードを数式で探る
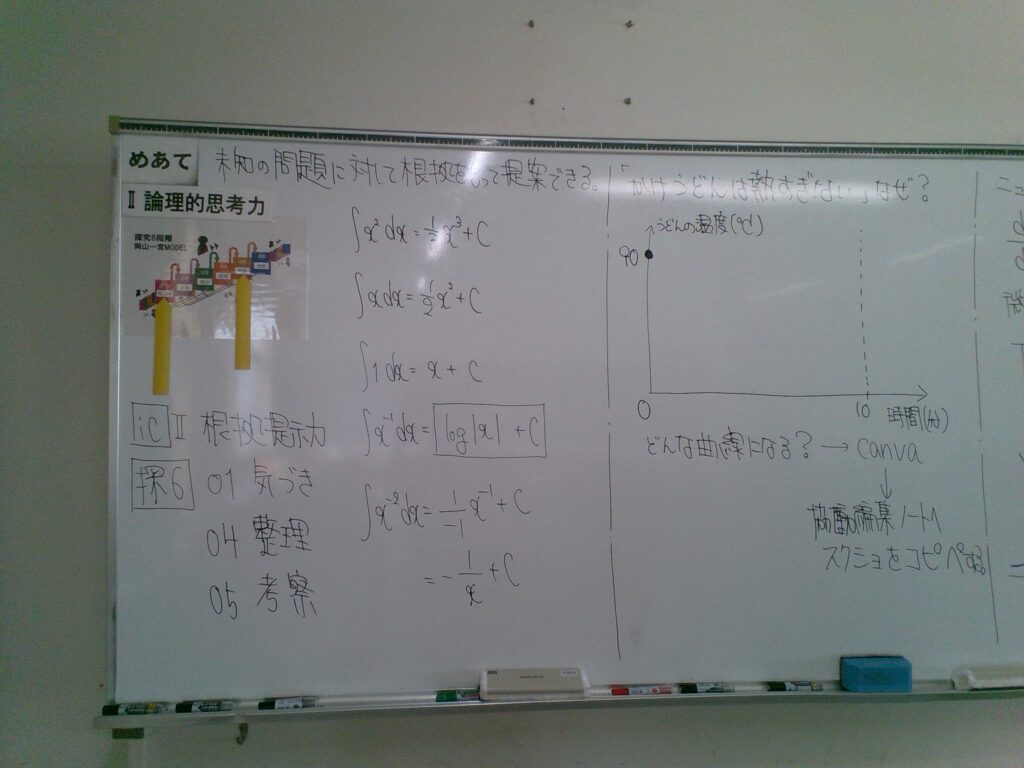
「かけうどんは熱いけれど、いつまでも熱すぎるわけではない」──そんな日常の疑問から、2年生の数学の授業がスタートしました。提供直後の温度を90度、室温を25度と設定し、10分間でどのように冷めていくかを班ごとにCanvaのホワイトボードで予想しました。
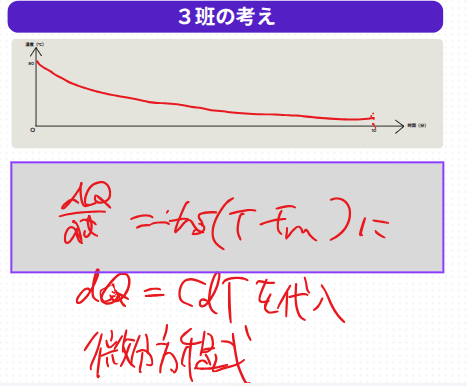
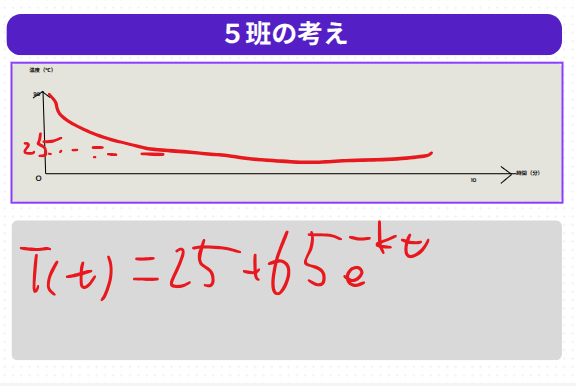
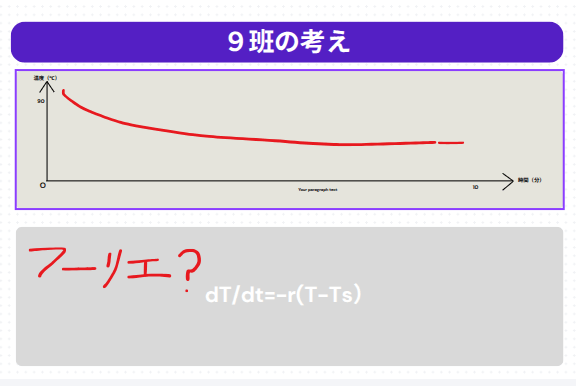
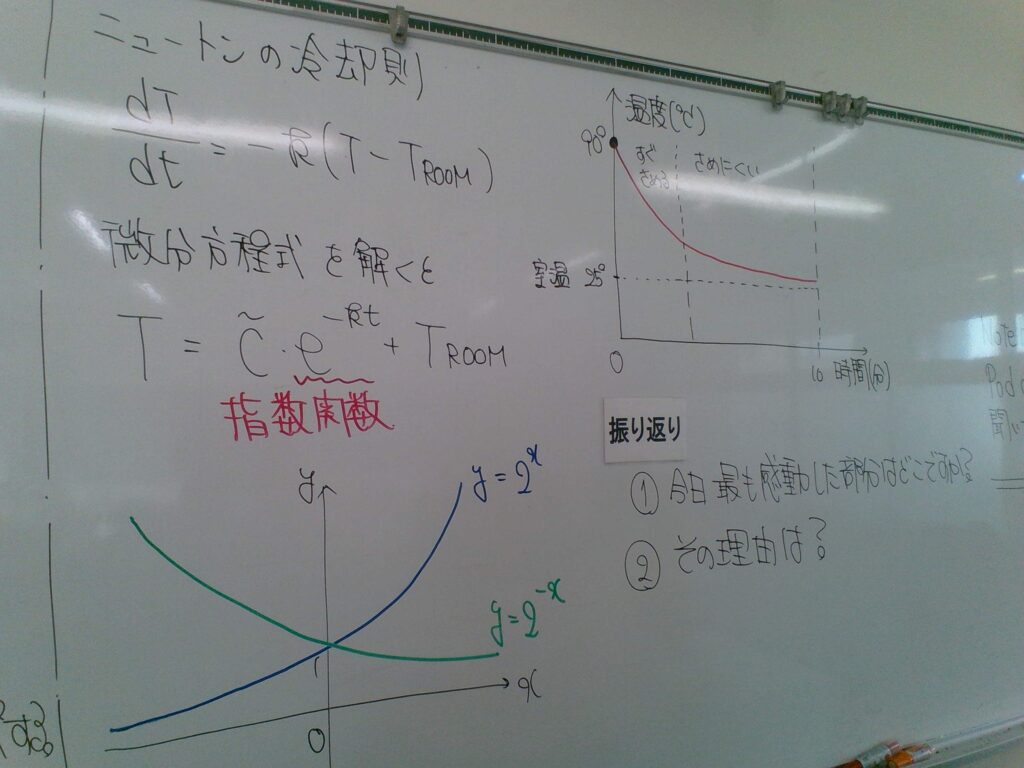
予想から発見へ:ニュートンの冷却則
予想を数式で説明する過程で、生徒たちはニュートンの冷却則という微分方程式にたどり着きました。解いてみると指数関数が現れ、最初は急激に冷めるが、その後は室温に近づきながらなかなか冷めにくいという現象を、数理的に理解できることが分かりました。
課題研究の姿勢を体感
この授業は「未知の問題に対して根拠を持って提案する」という課題研究を意識した構成でした。身近な現象を数理モデルで表すことを通じ、数学と日常世界のつながりを体感し、生徒たちは新しい学びの面白さを発見しました。
生徒の声:日常に潜む数理の驚き
振り返りでは、
- 「普段の生活を数式で説明できることに感動した」
- 「微分方程式が身近な現象に役立つことに驚いた」
- 「うどんの温度が室温を漸近線に近づくことに納得した」
といった声が多く挙がりました。生徒の気づきはまさに探究学習そのものでした。
学びを共有する新たな形
授業後には、協働編集ノートと振り返りのデータをNotebookLMに読み込み、ポッドキャストを作成しました。授業の概要や自分の振り返りに加え、他の生徒の考えも「ラジオ番組のような雰囲気」で聞くことができ、学びの共有がさらに広がりました。